TIN Simplify
Algorytm dzieli punkty na kwadratowe komórki, tak aby każdy punkt leżał w pojedynczej komórce. W pierwszym kroku pierwszy punkt jest pobierany z pierwszej komórki, zgodnie z kolejnością punktów w wejściowym pliku punktów lub chmurze punktów.
Wokół pierwszego punktu sprawdzane jest spełnienie warunku ∆h (Elevation difference) dla wszystkich sąsiednich punktów. Wszystkie punkty w danym promieniu, w tym te w sąsiednich komórkach, są uważane za punkty sąsiadujące (patrz rysunek poniżej).
Gdy wszystkie punkty z wyższą wartością ∆h niż wartość zdefiniowana przez użytkownika zostaną wykluczone, opisana procedura jest kontynuowana dla następnego punktu w pierwszej komórce. Następnie proces jest kontynuowany dla wszystkich punktów w sąsiedniej komórce w kierunku współrzędnej x i tak dalej do ostatniej komórki.
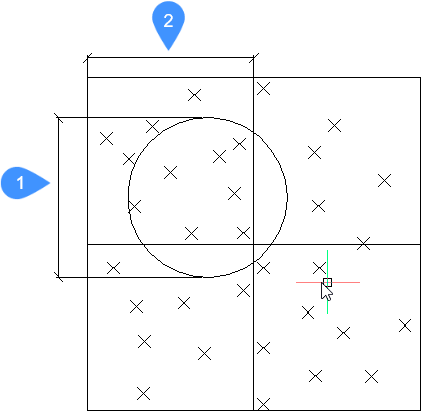
- Promień dla kroku uproszczenia
- Promień dla kroku uproszczenia
Algorytm automatycznie proponuje wartość parametru Radius for simplification step. Robi to poprzez obliczenie Bounding Box na podstawie podanych punktów wejściowych. Następnie przyjmuje większy z wymiarów ∆x i ∆y (długość i szerokość). Obliczane jest 0,5% uzyskanej wartości, która jest zaokrąglana i wyświetlana w wierszu poleceń jako proponowana wartość dla użytkownika.
Większy rozmiar komórki (tj. parametr Radius for simplification step ) zapewnia niższą dokładność końcowej powierzchni TIN. Aby uzyskać większą dokładność uproszczonej sieci TIN, bardziej sensowne jest wprowadzenie mniejszego rozmiaru komórki.

